Zwift racing teams using constraint programming

Zwift Racing Leage is a well established racing format on the online cycling platform. It has its fair share of critics, including me, but while better alternatives remain unavailable it’s the most straightforward way to get racing this winter.

As I’ve mentioned before this season the standard Zwift categories are being subdivided into “Dev” and “Standard” by two particular power characteristics. This means that in a cohort of riders, some might be only eligible for the lower team, some only for the higher team, and some for both.

This leaves the mugs (like me) who end up running a team with a problem:

You have a load of riders who want to race
We know in advance if they’re a yes/no/maybe for each of the six weeks
There can be a maximum of 12 people per team
For any given race, a maximum of six can ride
Ideally we want a minimum of four per race

You could try to solve this by hand using a spreadsheet, but this would almost certainly use a “greedy” approach. Assigning riders as you spot them leads to a local optimal solution (can’t get better than this without reversing all decisions), but is unlikely to find the overall (“global”) optimal solution.

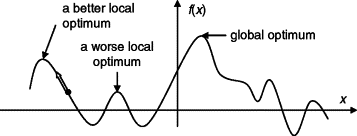
*Local vs global optima, borrowed from Fundamentals of Algorithms*

But this is actually a classic combinatorial optimisation problem. Constraint Programming (CP) searches across the entire solution space, propagating the constraints you set each time it tries to solve the problem, then backtracking and trying again until it finds the actual optimal solution.

Sounds complex, but Google’s OR-Tools package includes a CP solver, so we could leverage that to solve this problem:

import pandas as pd
from ortools.sat.python import cp_model

We’ll start by defining our data, where:

$R$ is the set of all riders
$K$ is the set of all races
$T$ is the set of potential teams
$D$ is the set of divisions

riders = ['Rider_1', 'Rider_2', 'Rider_3', 'Rider_4', 'Rider_5', 'Rider_6',
          'Rider_7', 'Rider_8', 'Rider_9', 'Rider_10', 'Rider_11', 'Rider_12',
          'Rider_13', 'Rider_14', 'Rider_15', 'Rider_16', 'Rider_17', 'Rider_18']
races = ['Race_1', 'Race_2', 'Race_3', 'Race_4', 'Race_5', 'Race_6']
potential_teams = ['Team_1', 'Team_2', 'Team_3']
divisions = ['Top', 'Bottom']

Then add rider eligibility and availability:

Eligible( $r$ , $d$ ): 1 if rider $r \in R$ is eligible for division $d \in D$ , 0 otherwise
Avail_Yes( $r$ , $k$ ): 1 if rider $r \in R$ is a “Yes” for race $k \in K$ , 0 otherwise
Avail_Maybe( $r$ $k$ ): 1 if rider $r \in R$ is a “Maybe” for race $k \in K$ , 0 otherwise

eligibility = {
        'Rider_1':  {'Top': 0, 'Bottom': 1}, 
        'Rider_2':  {'Top': 1, 'Bottom': 1},
        'Rider_3':  {'Top': 1, 'Bottom': 1}, 
        'Rider_4':  {'Top': 1, 'Bottom': 1},
        'Rider_5':  {'Top': 1, 'Bottom': 1}, 
        'Rider_6':  {'Top': 1, 'Bottom': 1},
        'Rider_7':  {'Top': 1, 'Bottom': 1}, 
        'Rider_8':  {'Top': 1, 'Bottom': 0},
        'Rider_9':  {'Top': 1, 'Bottom': 0}, 
        'Rider_10': {'Top': 1, 'Bottom': 0},
        'Rider_11': {'Top': 1, 'Bottom': 0}, 
        'Rider_12': {'Top': 1, 'Bottom': 0},
        'Rider_13': {'Top': 1, 'Bottom': 1}, 
        'Rider_14': {'Top': 1, 'Bottom': 0},
        'Rider_15': {'Top': 1, 'Bottom': 0},
        'Rider_16': {'Top': 1, 'Bottom': 0},
        'Rider_17': {'Top': 1, 'Bottom': 0},
        'Rider_18': {'Top': 1, 'Bottom': 1}
    }
    
availability_yes = {
        'Rider_1':  [0, 1, 1, 1, 0, 0], 
        'Rider_2':  [1, 1, 1, 1, 1, 1],
        'Rider_3':  [0, 1, 1, 0, 0, 0],
        'Rider_4':  [0, 0, 0, 0, 0, 0],
        'Rider_5':  [0, 0, 1, 1, 1, 1],
        'Rider_6':  [1, 1, 1, 1, 1, 1],
        'Rider_7':  [1, 0, 0, 1, 0, 1],
        'Rider_8':  [0, 1, 1, 1, 1, 1],
        'Rider_9':  [1, 0, 1, 1, 1, 1],
        'Rider_10': [1, 1, 1, 1, 1, 1],
        'Rider_11': [1, 0, 1, 1, 0, 1],
        'Rider_12': [1, 0, 0, 0, 1, 1],
        'Rider_13': [1, 0, 1, 1, 0, 1],
        'Rider_14': [1, 1, 1, 0, 1, 1],
        'Rider_15': [1, 1, 1, 1, 1, 1],
        'Rider_16': [1, 1, 1, 1, 1, 1],
        'Rider_17': [0, 0, 1, 0, 1, 1],
        'Rider_18': [1, 1, 1, 1, 1, 1]
    }
  
availability_maybe = {
        'Rider_1':  [0, 0, 0, 0, 1, 1],
        'Rider_2':  [1, 1, 1, 1, 1, 1],
        'Rider_3':  [0, 0, 0, 0, 1, 1], 
        'Rider_4':  [0, 0, 0, 1, 1, 1],
        'Rider_5':  [0, 1, 0, 0, 0, 0], 
        'Rider_6':  [0, 0, 0, 0, 0, 0],
        'Rider_7':  [0, 1, 1, 0, 1, 0],
        'Rider_8':  [0, 0, 0, 0, 0, 0],
        'Rider_9':  [0, 0, 0, 0, 0, 0],
        'Rider_10': [0, 0, 0, 0, 0, 0],
        'Rider_11': [0, 1, 0, 0, 1, 0],
        'Rider_12': [0, 0, 0, 0, 0, 0],
        'Rider_13': [0, 1, 0, 0, 0, 0],
        'Rider_14': [0, 0, 0, 0, 0, 0], 
        'Rider_15': [0, 0, 0, 0, 0, 0],
        'Rider_16': [0, 0, 0, 0, 0, 0],
        'Rider_17': [0, 0, 0, 0, 0, 0],
        'Rider_18': [0, 0, 0, 0, 0, 0]
    }

And add some hard input contraints that we can maninpulate for debugging.

MIN_RIDERS_PER_RACE = 3
MAX_RIDERS_PER_RACE = 6
MAX_RIDERS_PER_TEAM = 12
MIN_TEAMS_TO_CREATE = 2
MAX_TEAMS_TO_CREATE = 3

Before we try to solve the problem, lets run some sanity checks to ensure that at least one solution will exist:

# Check there is at least enough availability for each race day
for k_idx, k in enumerate(races):
    yes_count = 0
    for r in riders:
        if availability_yes[r][k_idx] == 1:
            yes_count += 1
    print(f"{k}: {yes_count} total 'Yes' riders.")
    if yes_count < MIN_TEAMS_TO_CREATE * MIN_RIDERS_PER_RACE:
        print(f"  !! WARNING: Only {yes_count} 'Yes' riders for {k}. ")
        print(f"     This is less than (min_teams * min_riders_per_race), ")
        print(f"     which is {MIN_TEAMS_TO_CREATE * MIN_RIDERS_PER_RACE}.")

Race_1: 12 total 'Yes' riders.
Race_2: 10 total 'Yes' riders.
Race_3: 15 total 'Yes' riders.
Race_4: 13 total 'Yes' riders.
Race_5: 12 total 'Yes' riders.
Race_6: 15 total 'Yes' riders.

# Check there's enough eligible riders for each division
top_only_riders = [r for r in riders if eligibility[r]['Top'] == 1 and eligibility[r]['Bottom'] == 0]
bottom_only_riders = [r for r in riders if eligibility[r]['Top'] == 0 and eligibility[r]['Bottom'] == 1]
either_riders = [r for r in riders if eligibility[r]['Top'] == 1 and eligibility[r]['Bottom'] == 1]

print(f"Top-only riders:         {len(top_only_riders)}")
print(f"Bottom-only riders:      {len(bottom_only_riders)}")
print(f"Either riders:           {len(either_riders)}")
print(f"Total 'Top' eligible:    {len(top_only_riders) + len(either_riders)}")
print(f"Total 'Bottom' eligible: {len(bottom_only_riders) + len(either_riders)}")

Top-only riders:         9
Bottom-only riders:      1
Either riders:           8
Total 'Top' eligible:    17
Total 'Bottom' eligible: 9

# Now check by race and eligibility

eligible_groups = {
    "Top": top_only_riders + either_riders,
    "Bottom": bottom_only_riders + either_riders
}

found_critical_issue = False

# Loop over both divisions
for division, eligible_riders in eligible_groups.items():
    
    print(f"\n--- Checking '{division}' Division ---")
    
    if not eligible_riders:
        print(f"  !! WARNING: No riders are eligible for '{division}' division at all!")
        found_critical_issue = True
        continue

    # Loop over all races
    for k_idx, k_name in enumerate(races):
        
        # Count 'Yes' riders for this specific division and race
        core_yes_count = 0
        for r in eligible_riders:
            if availability_yes[r][k_idx] == 1:
                core_yes_count += 1
        
        print(f"  {k_name}: {core_yes_count} '{division}' eligible riders with 'Yes' status.")


--- Checking 'Top' Division ---
  Race_1: 12 'Top' eligible riders with 'Yes' status.
  Race_2: 9 'Top' eligible riders with 'Yes' status.
  Race_3: 14 'Top' eligible riders with 'Yes' status.
  Race_4: 12 'Top' eligible riders with 'Yes' status.
  Race_5: 12 'Top' eligible riders with 'Yes' status.
  Race_6: 15 'Top' eligible riders with 'Yes' status.

--- Checking 'Bottom' Division ---
  Race_1: 5 'Bottom' eligible riders with 'Yes' status.
  Race_2: 5 'Bottom' eligible riders with 'Yes' status.
  Race_3: 7 'Bottom' eligible riders with 'Yes' status.
  Race_4: 7 'Bottom' eligible riders with 'Yes' status.
  Race_5: 4 'Bottom' eligible riders with 'Yes' status.
  Race_6: 6 'Bottom' eligible riders with 'Yes' status.

Now we’ll define our model, and the variables it must find values for:

$x_{r, t}$ : 1 if Rider $r$ is assigned to Team $t$ , 0 otherwise
$z_{t, d}$ : 1 if Team $t$ is assigned to Division $d$ , 0 otherwise
$y_{t}$ : 1 if Team $t$ is created), 0 otherwise

model = cp_model.CpModel()

x = {}
for r in riders:
    for t in potential_teams:
        x[r, t] = model.NewBoolVar(f'x_{r}_{t}')

z = {}
for t in potential_teams:
    for d in divisions:
        z[t, d] = model.NewBoolVar(f'z_{t}_{d}')

y = {}
for t in potential_teams:
    y[t] = model.NewBoolVar(f'y_{t}')

Now lets set the constraints our solver must obey:

One team per rider
- $\sum_{t \in T} x_{r, t} \leq 1$ for each rider $r \in R$
Number of teams
- $Min_Teams \leq \sum_{t \in T} y_{t} \leq Max_Teams$
One division per team
- $\sum_{d \in D} z_{t, d} = y_{t}$
Maximum team size
- $\sum_{r \in R} x_{r, t} \leq Max_Roster . y_{t}$ for each team $t \in T$
A rider can only be on a team if eligible for that division, and the team has been assigned
- $x_{r, t} + z_{t, d} \leq 1 + Eligible (r, d)$ for all $r \in R, t \in T, d \in D$ .
For each race day, there must be at least enough “yes” only, and not too many “yes” and “maybe” combined, so everyone who wants to gets to race:
- $\sum_{r \in R} x_{r, t} . Avail_Yes (r, k) \geq Min_Team_Size . y_{t}$
- $\sum_{r \in R} x_{r, t} . (Avail_Yes (r, k) + Avail_Maybe (r, k) \leq Max_Team_Size . y_{t}$

# 1. A rider can be on at most one team.
for r in riders:
    model.Add(sum(x[r, t] for t in potential_teams) <= 1)

# 2. We want to enter 2 or 3 teams.
model.AddLinearConstraint(sum(y[t] for t in potential_teams),
                          MIN_TEAMS_TO_CREATE, MAX_TEAMS_TO_CREATE)

# 3. An active team must be in exactly one division.
for t in potential_teams:
    model.Add(sum(z[t, d] for d in divisions) == y[t])

# 4. Team roster size
for t in potential_teams:
    model.Add(sum(x[r, t] for r in riders) <= MAX_RIDERS_PER_TEAM * y[t])

# 5. Rider eligibility.
for r in riders:
    for t in potential_teams:
        for d in divisions:
            if eligibility[r][d] == 0: 
                model.AddBoolOr([x[r, t].Not(), z[t, d].Not()])

# 6. Race day min/max
for t in potential_teams:
    for k_idx, k in enumerate(races):
        
        # Part A: The "Core" Minimum (yes only)
        core_riders_available = []
        for r in riders:
            if availability_yes[r][k_idx] == 1:
                core_riders_available.append(x[r, t])
        model.Add(sum(core_riders_available) >= MIN_RIDERS_PER_RACE * y[t])

        # Part B: The "Total" Maximum (yes and maybe)
        total_riders_available = []
        for r in riders:
            if (availability_yes[r][k_idx] == 1 or 
                availability_maybe[r][k_idx] == 1):
                total_riders_available.append(x[r, t])
        model.Add(sum(total_riders_available) <= MAX_RIDERS_PER_RACE * y[t])

Lastly, lets define our objective function. We want to get as many people racing as often i.e. $Maximise \sum_{r \in R} \sum_{t \in T} x_{r, t}$ :

all_assignments = []
for r in riders:
    for t in potential_teams:
        all_assignments.append(x[r, t])
model.Maximize(sum(all_assignments))

And now solve the problem:

solver = cp_model.CpSolver()
status = solver.Solve(model)

This outputs nothing… we’ll need to extract the results. We’ll create something that tells us the answer if a solution has been found, or point us in the direction of variables to change if not:

if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
    # We have an answer!
    
    print(f"Solution Found! Status: {solver.StatusName(status)}")
    print(f"Total Riders Assigned: {int(solver.ObjectiveValue())} / {len(riders)}")
    
    assigned_riders = set()

    # Loop through each potential team to see if it was created
    for t in potential_teams:
        
        # Check if this team was activated (y[t] == 1)
        if solver.Value(y[t]) == 0:
            continue
            
        # Find the team's assigned division
        team_division = ""
        for d in divisions:
            if solver.Value(z[t, d]) == 1:
                team_division = d
                
        # Find all riders assigned to this team
        team_roster = []
        for r in riders:
            if solver.Value(x[r, t]) == 1:
                team_roster.append(r)
                assigned_riders.add(r)
        
        # Print the team report
        print("\n")
        print(f"--- {t} (Assigned to: {team_division}) ---")
        print(f"Roster ({len(team_roster)} riders / {MAX_RIDERS_PER_TEAM} max):")
        print(", ".join(team_roster))
        
        # Print the race-by-race availability check for this team
        print("\nRace day availability:")
        for k_idx, k in enumerate(races):
            core_count = 0
            total_count = 0
            for r in team_roster:
                if availability_yes[r][k_idx] == 1:
                    core_count += 1
                if (availability_yes[r][k_idx] == 1 or 
                    availability_maybe[r][k_idx] == 1):
                    total_count += 1
                    
            print(f"  {k}: {core_count} firm yes, "
                  f"{total_count} including maybes")
    
    # Print Unassigned Riders
    unassigned = [r for r in riders if r not in assigned_riders]
    if unassigned:
        print(f"--- Unassigned Riders ({len(unassigned)}) ---")
        print(", ".join(unassigned))
    else:
        print("\n")
        print("--- All riders assigned to a team! ---")

elif status == cp_model.INFEASIBLE:
    # We don't have an answer :(
    
    print("!! PROBLEM IS INFEASIBLE !!")
    print("No solution exists with the current rules.")
    print("\n--- CURRENT SETTINGS ---")
    print(f"  MIN_RIDERS_PER_RACE: {MIN_RIDERS_PER_RACE}")
    print(f"  MAX_RIDERS_PER_RACE: {MAX_RIDERS_PER_RACE}")
    print(f"  MAX_RIDERS_PER_TEAM: {MAX_RIDERS_PER_TEAM}")
    print(f"  MIN_TEAMS_TO_CREATE: {MIN_TEAMS_TO_CREATE}")
    print("\n--- WHAT TO DO NEXT ---")
    print("1. Check the sanity checks for critical warnings")
    print("2. Go back to the debugging constants and make the rules easier")
    print("3. Re-run with new constraints")
    
else:
    print(f"Solver finished with status: {solver.StatusName(status)}")

Solution Found! Status: OPTIMAL
Total Riders Assigned: 18 / 18


--- Team_1 (Assigned to: Bottom) ---
Roster (6 riders / 12 max):
Rider_1, Rider_2, Rider_4, Rider_5, Rider_13, Rider_18

Race day availability:
  Race_1: 3 firm yes, 3 including maybes
  Race_2: 3 firm yes, 5 including maybes
  Race_3: 5 firm yes, 5 including maybes
  Race_4: 5 firm yes, 6 including maybes
  Race_5: 3 firm yes, 5 including maybes
  Race_6: 4 firm yes, 6 including maybes


--- Team_2 (Assigned to: Top) ---
Roster (6 riders / 12 max):
Rider_3, Rider_6, Rider_7, Rider_8, Rider_10, Rider_11

Race day availability:
  Race_1: 4 firm yes, 4 including maybes
  Race_2: 4 firm yes, 6 including maybes
  Race_3: 5 firm yes, 6 including maybes
  Race_4: 5 firm yes, 5 including maybes
  Race_5: 3 firm yes, 6 including maybes
  Race_6: 5 firm yes, 6 including maybes


--- Team_3 (Assigned to: Top) ---
Roster (6 riders / 12 max):
Rider_9, Rider_12, Rider_14, Rider_15, Rider_16, Rider_17

Race day availability:
  Race_1: 5 firm yes, 5 including maybes
  Race_2: 3 firm yes, 3 including maybes
  Race_3: 5 firm yes, 5 including maybes
  Race_4: 3 firm yes, 3 including maybes
  Race_5: 6 firm yes, 6 including maybes
  Race_6: 6 firm yes, 6 including maybes


--- All riders assigned to a team! ---

Victory!

However despite all this, we settled on just running one top and one bottom division team, simply because people are far too flakey for this to work in real life…